Why Do We Need Neural Networks with Hidden Layers?
This text was inspired by the section "Activation functions" in Google's Machine Learning Crash Course and a blog post mentioned in that section. I decided to explain the rationale of all this to myself.
Let's say we have a number of features and a binary classification task (e.g. whether a house will be sold, based on two features: its price and area). In case of two features, we can visualize them on a 2D graph and the task would be to calculate a formula for a straight line that separates our two classes. We do so by multiplying each value of a feature by a certain floating point number (weight) and then adding some floating point scalar number to the whole graph equation (that basically lifts or lowers the line on our graph), which is called bias. We get a straight line that has some slope (determined by weights) and crosses Y axis in some point (determined by bias).
(If we have three features, then instead of a straight line, we get a plane. For more than 3 features, we get a hyperplane.)
In many cases there is no straight line that can separate instances of two classes.
Source: O'Reilly
To try and fix this, we can produce a feature cross, for example multiplying [square of] one feature by [square of] another (it is possible, since all features, even categorical ones, are represented as numbers). We still have a linear equation, but the line now looks curvy (or it's a hyperbolic line, so looks like two separate curvy lines). Since the equation is still linear, we can imagine that in a space with more dimensions, there is a perfectly flat plane or hyperplane separating two original features. We can try and create feature crosses by hand, adjusting weights now not only for original features, but for their crosses as well.
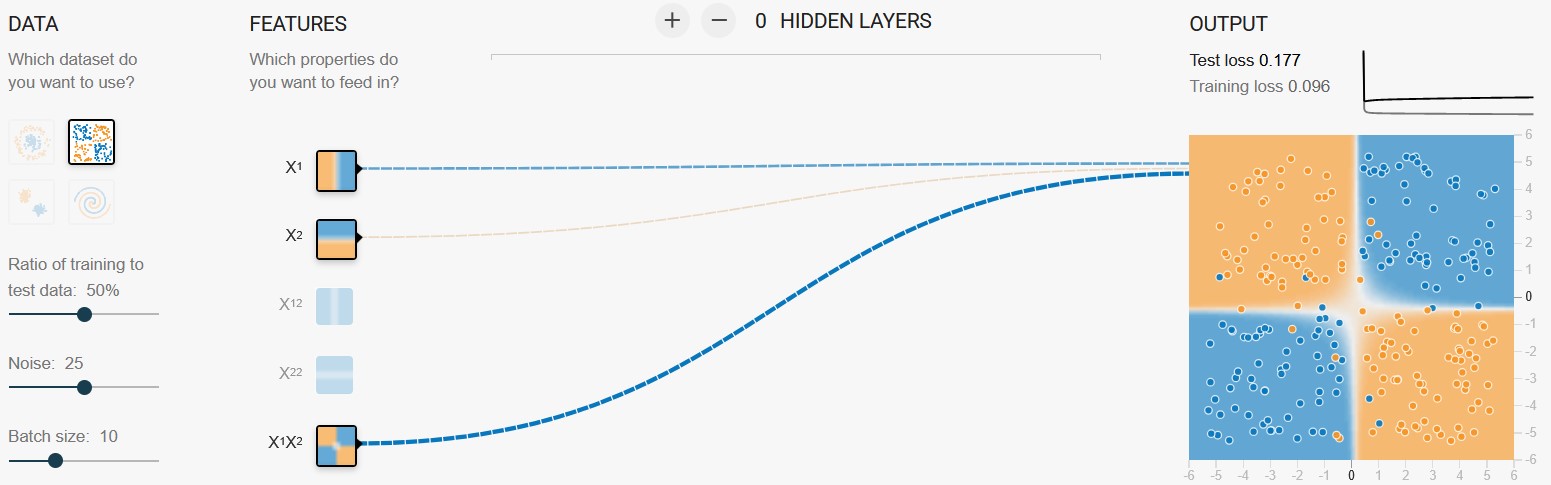This feature cross works well. Screenshot from TensorFlow Playground
But feature crosses aren't enough for complex dependencies.
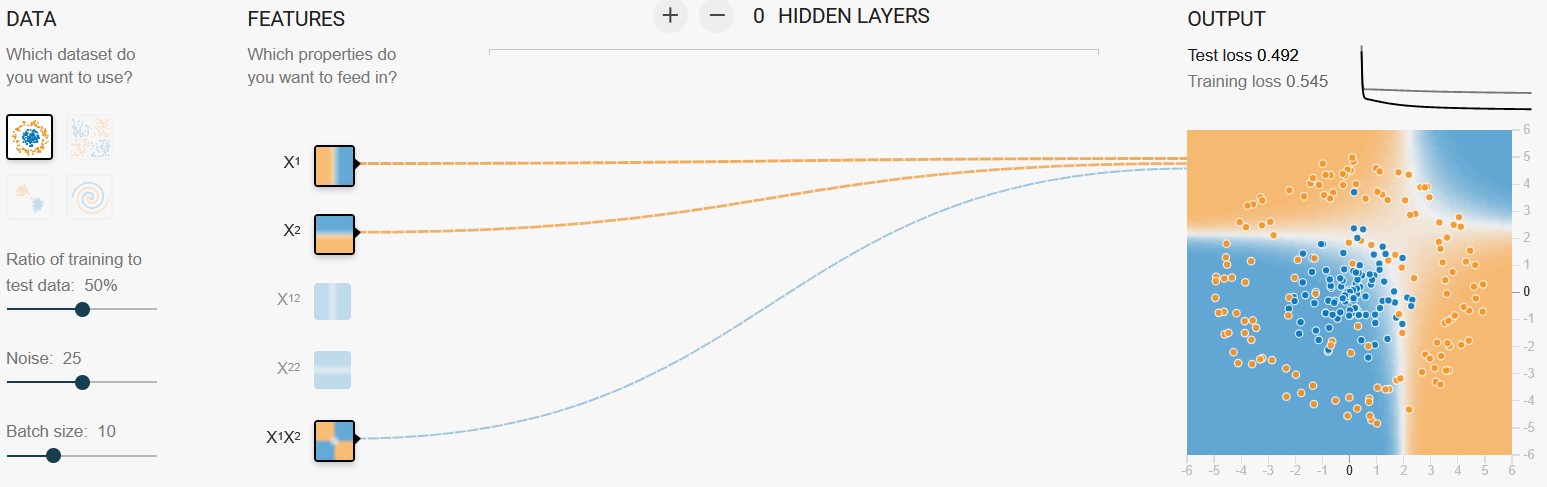Here, a feature cross doesn't work well. Screenshot from TensorFlow Playground
Just like we previously asked the model to figure out the weights and bias on its own, we can now ask it to create abstract combinations of features on its own as well and see if it helps separate data points.
This process can't be done with a simple model layout of one input layer and one output layer. So we create "hidden" layers, in which our model creates abstract interactions between inputs, adjusts their weights, adds bias, feeds them to subsequent hidden layers where new abstractions are created, and so on.
(If our features can be separated by one continuous function, one hidden layer will always be enough, as long as it has enough neurons. But even then we might choose to have multiple layers for efficiency. To work with hierarchical structures, e.g. put together edges into shapes, then shapes into objects that we need to recognize in an image, we definitely need multiple hidden layers.)
Okay, so we have added some layers. Despite our space of features now being multidimensional and transformations looking very complex, without an additional operation its predictions will only work with linear dependencies between features.
To address this problem, at each layer we introduce a function called activation function. The model takes the bias summed with all products of values and weights and feeds them to this function. If the activation function is non-linear, our model gets the ability to work with non-linear dependencies.
Popular examples of activation functions are Sigmoid (more correctly, logistic, since "sigmoid" is too general a term; produces values between 0 and 1), tanh (short for "hyperbolic tangent"; also an S-shaped function, like sigmoid, and produces values between -1 and 1) and ReLU (short for "Rectified Linear Unit", produces 0 for negative values and preserves original value for positive ones). Usually, the same activation function is applied to all hidden layers, then a task-specific function (could be same, could be different) is applied to outputs of the last hidden layer to produce the final output of the model.
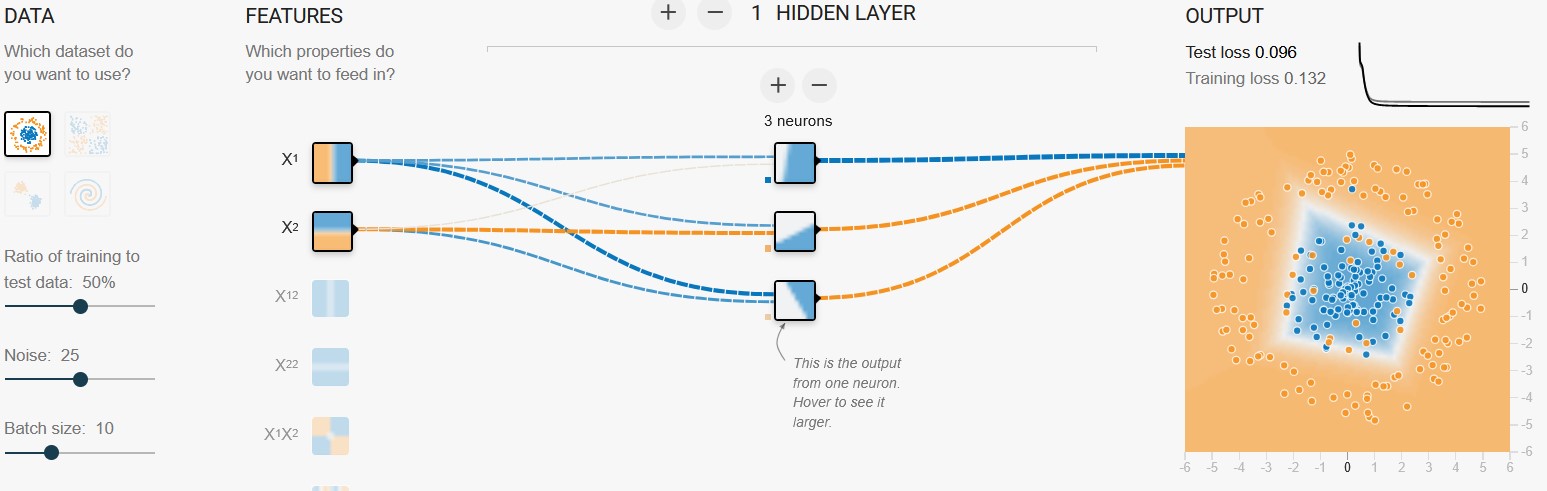Problem solved with one hidden layer and ReLU activation function. Screenshot from TensorFlow Playground
ReLU is often favored over sigmoid and tanh because it can be computed faster and avoids the so-called "vanishing gradient" problem (vanishing gradients occur when small weight updates during training make the model stop learning). There is, however, a "Dead ReLU Units" problem.
Now our model creates and weighs certain combinations of inputs (much more abstract equivalents of a feature cross we would add manually in our simple model). Before moving on to the next layer, the model applies an activation function.
In the process, the model warps and reshapes our space of feature values, sometimes even tearing it apart (scientifically speaking, breaking its topology). Our model strives to create a certain multidimensional space where data points will all be separated by a "straight line", i.e. where the equation finally becomes linear.
A side note: when I say "warps and reshapes our space", it could imply some sort of distortion. However, according to the manifold hypothesis, it's the other way round: a neural network "unfolds" a "manifold", which is a lower-dimensional structure embedded in high-dimensional space, like a crumpled paper in 3D, to produce a linearly separable representation.
This means that in the picture above, where we see some sort of parallelogram, it's actually a hyperplane in a higher-dimensional space.
Here is a beautiful visualization from this blog post, where two spirals are getting separated from each other after some "warping and reshaping" of the space:
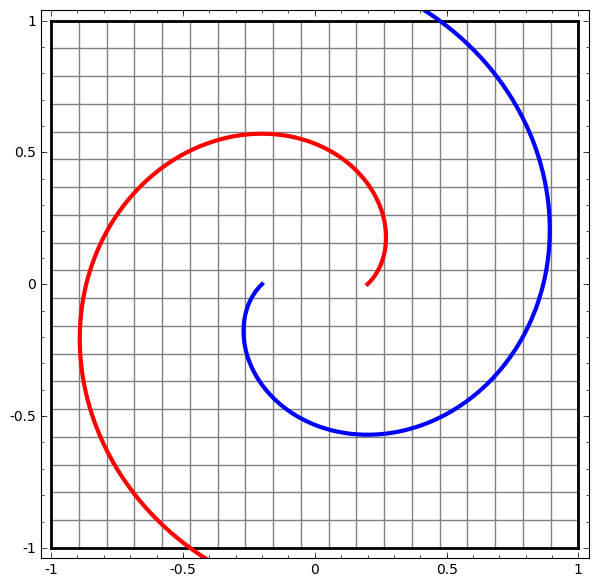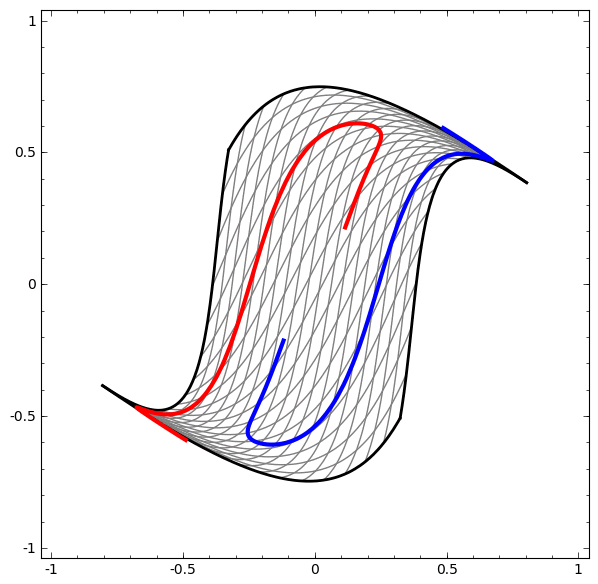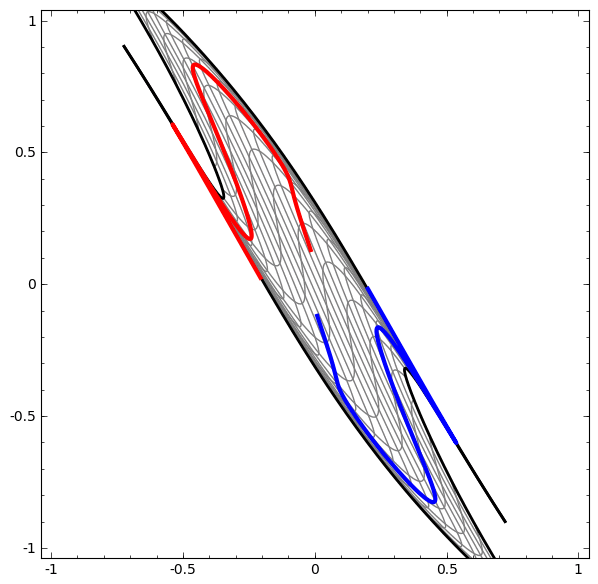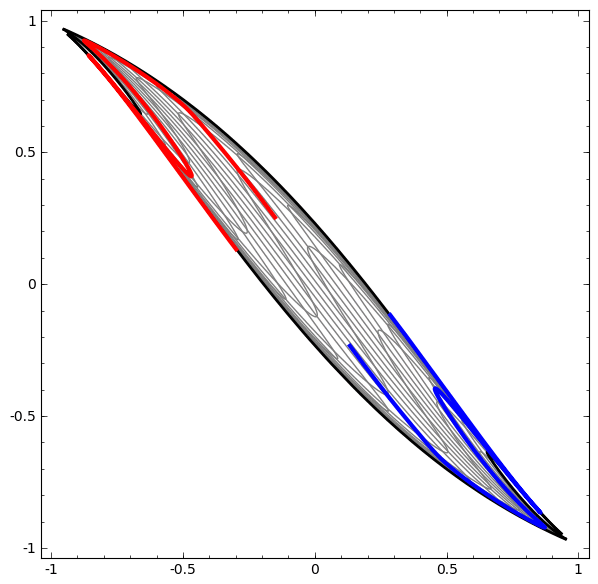
And now, the final step. When, after much learning, a multidimensional space is created, in which data points are more or less successfully separated, a task-dependent activation function (e.g. sigmoid for binary classification, softmax for multi-class) is applied one last time. It converts the linear separation in the transformed space into a probabilistic output, ensuring the output is interpretable. This is the prediction we asked for.